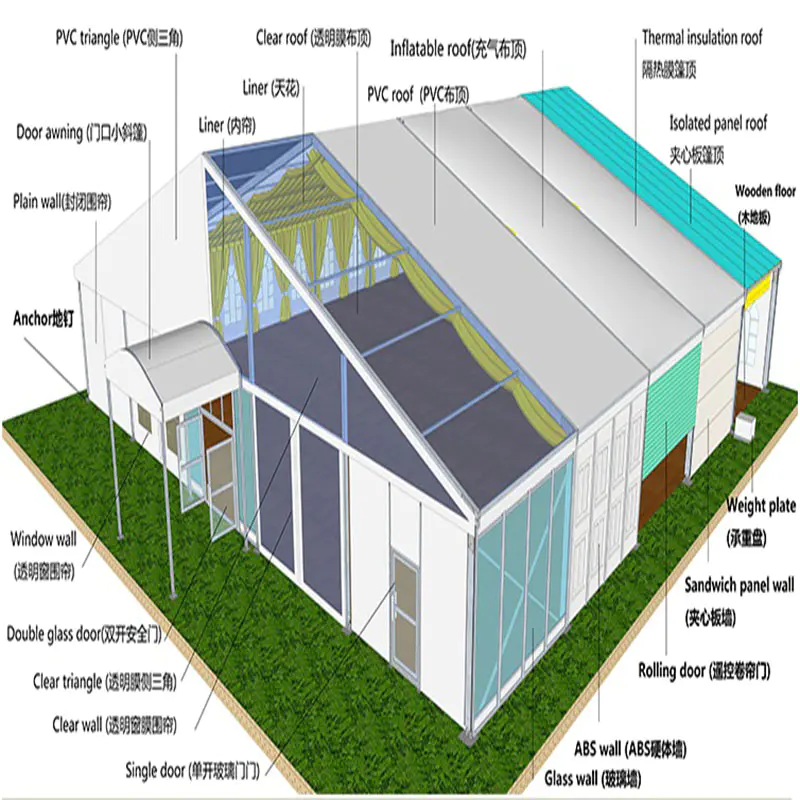
How to Calculate Geodesic Domes

The ground wire dome was promoted by Buckminster Fuller in the 1950 s.Since its launch, the ground wire dome has been built for a variety of uses, including residential, container and outer space structures.The name of the dome comes from the chord that creates the structure of the large arc, also known as the ground wire.
The form of the dome is useful because it is approximately spherical and has a large volume relative to its surface area.In addition, the chord of the structure distributes the load around the internal volume like the shell.There are many kinds of ground wire spheres, each of which has unique geometric properties.
The formula for calculating most spheres is too complicated to include here, so the construction specifications are determined using the provided references and resources.Nevertheless, two very popular types of ground wire domes are given below.Determine the purpose of the ground dome and the size of the dome.
Because the dome is spherical, the diameter or radius is the right way to describe the size.After determining the size, find the required type of ground wire dome from the references and resources.For simplicity, two types of domes are described here-Twenty-plane body and truncated twenty-plane body.
Both types are made up of regular polygons.There are 20 faces in the 20-sided body, consisting of an equilateral triangle.Although it is loosely close to a sphere, the twenty faces are easy to construct and can contain many variations.
According to the required form, the Dome of the twenty-sided body earth wire omits 1, 5 or 15 faces from the twenty-sided body.To calculate the string length, determine the maximum external radius or the minimum internal radius of the polygon.The maximum external radius will give the size of the floor area of the structure, and the minimum internal radius represents the available volume of the dome.
String length = maximum outer radius/0.
String length = minimum inner radius/0.
There is only one string length in the Dome of the twenty-sided body Earth survey, so the calculation is complete.A complete twenty-plane body has 20 faces, 30 strings, 12 vertices or nodes.The cut-off angle twenty-sided body ground wire dome is a very popular form of the ground wire dome.
From its name, the type of dome of this ground wire is created from the modified twenty-sided body.The truncated twenty faces have 32 faces, 90 strings, and 60 vertices or nodes.Unlike the twenty-sided body, the truncated twenty-sided body consists of two shapes--Straight hexagon and five horns.
As with the twenty-sided body survey Earth dome, the string length of the truncated twenty-sided body survey Earth dome relative to the radius can be found.String length = maximum outer radius/2.String length = minimum inner radius/2.Although the truncated twenty-plane body has only one string length, it is recommended to triangulate the positive hexagon and the five angles.The easiest way to do this is to construct the hexagon and The Five Corners with an equilateral triangle.
The hexagon will not be affected by the introduction of equilateral triangles, but five yuan constructed with equilateral triangles will expand three-In size, break the plane of the perimeter sphere.If not, a second string length can be introduced to triangulate the Pentagon with an isosceles triangle.Internal 5-angle chord = external 5-angle chord/1.
Otherwise, the string length can approximate the shape of the sphere.This formula will apply to any chord in the form of a ground wire close to the sphere.After calculating the chord, test the calculation by making the balsa or basswood scale model of the ground wire dome.
Direct selling is used for vertex or chord intersections.Keep in mind that chords are calculated according to lines with no dimensions.Find the depth of the join from the vertex and multiply that dimension by 2.
Subtract this from the calculated string length, which is the scaling length the model wants to cut